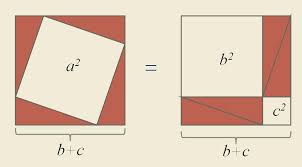
Pese a que las Matemáticas ya eran avanzadas en tiempos anteriores (babilonios o egipcios), hasta los griegos, la preocupación por esta ciencia era meramente práctica: medir, construir, contar,... Los griegos, sin embargo, se preocupan por reflexionar sobre la naturaleza de los números, sobre la naturaleza de los "objetos" matemáticos (geometría),... Convirtieron las Matemáticas en una ciencia racional y estructurada, con propiedades que se demuestran. En realidad, la contribución de los griegos a las MATEMÁTICAS constituye el mayor avance de esta ciencia en el periodo comprendido entre la Prehistoria y el Renacimiento. La Escuela Jónica fundada por TALES DE MILETO (en torno al 600 a.C.), fue la primera en comenzar el estudio científico de la Geometría. Se le atribuyen las primeras demostraciones de teoremas geométricos mediante el razonamiento lógico. Más tarde fue la Escuela Pitagórica fundada por PITÁGORAS (en torno al 550 a.C.). Se le atribuyen numerosos descubrimientos matemáticos, entre otros, la demostración del conocido Teorema de Pitágoras : "En un triángulo rectángulo, LA HIPOTENUSA al cuadrado es igual a la suma de los cuadrados de los catetos."
Además, los pitagóricos elaboraron un primer grupo de cuatro disciplinas matemáticas: la aritmética, la música (o aritmética de intervalos musicales ), la geometría plana y la geometría esférica. La doctrina pitagórica sostenía que todas las razones que rigen el mundo debían ser razones de números enteros o fraccionarios; estos puntos de vista fueron combatidos por otra escuela griega importante: la escuela Elea; su crítica tomó la forma en los trabajos de Parménides y las célebres paradojas de Zenón. Después, podemos citar la Primera Escuela de Alejandría cuyo principal representante fue EUCLIDES (300 a.C.). Uno de los personajes que más han influido en la historia de las matemáticas. Su obra más importante es el tratado LOS ELEMENTOS, cuyo contenido y estructura se ha estudiado en las escuelas y universidades hasta hace muy poco, y fue trascendental en el desarrollo de la geometría. El método euclidiano comprende, en primer lugar, una teoría general fundada sobre axiomas (propiedades que admitimos como ciertas sin necesidad de demostración por ser evidentes). Euclides llamó a sus axiomas postulados.
Citemos, para finalizar este breve recorrido a ARQUÍMEDES (285 a.C.). Fue el mayor matemático de la antigüedad. Se le atribuye : el calculo de p por aproximaciones sucesivas, la determinación de los volúmenes del cilindro y de la esfera, la cuadratura del segmento de la parábola, el empleo de los momentos estáticos y de los centros de gravedad, etc... . Estos descubrimientos abrieron el camino a la mecánica y al cálculo integral. Después de un largo intervalo durante el cual los progresos son escasos, surge otro fructífero periodo debido a la Segunda Escuela de Alejandría (100-300 d.C.) en la que destacan: Nicóman, Ptolomeo (con su célebre sistema del mundo), Diofanto (con sus grandes investigaciones aritméticas) y Pappus (con su obra "Colección"). A partir de este momento, la ciencia helénica comienza a declinar. En occidente la huella de la cultura griega fue casi inexistente durante muchos años. El interés de los romanos por las matemáticas griegas se redujo a las aplicaciones prácticas de las mediciones de terrenos y cálculos y las obras griegas no se tradujeron al latín. Fue el mundo árabe el que recogió el testigo de las matemáticas griegas.
PROBLEMAS CLÁSICOS DE GRECIA LA CUADRATURA DEL CIRCULO
Consiste en construir un cuadrado de área igual a un círculo dado. Si tenemos un círculo de radio conocido R, su área es la que aparece en la figura p.R2 y hay que buscar un cuadrado que tenga el área igual (como en la figura). Como hemos dicho este problema no tiene solución con regla y compás. Lindenman (1852-1939), un matemático alemán, demostró que era imposible construirlo exactamente con regla y compás.

LA DUPLICACIÓN DEL CUBO
Consiste en construir el lado de un cubo cuyo volumen sea el doble del volumen del cubo inicial. Para eso habría que construir un segmento de longitud igual a la raíz cúbica de 2. Y esto es imposible utilizando solamente regla y compás.
No hay comentarios:
Publicar un comentario