El nacimiento del cálculo: El Cálculo constituye una de las grandes conquistas intelectuales de la humanidad. Una vez construido, la historia de la matemática ya no fue igual: la geometría, el álgebra y la aritmética, la trigonometría, se colocaron en una nueva perspectiva teórica. Detrás de cualquier invento, descubrimiento o nueva teoría, existe, indudablemente, la evolución de ideas que hacen posible su nacimiento.
• El Cálculo cristaliza conceptos y métodos que la humanidad estuvo tratando de dominar por más de veinte siglos. Una larga lista de personas trabajaron con los métodos "infinitesimales" pero hubo que esperar hasta el siglo XVII para tener la madurez social, científica y matemática que permitiría construir el Cálculo que utilizamos en nuestros días.
HISTORIA DEL CÁLCULO
INVENTORES DEL CÁLCULO: • Newton y Leibniz son considerados los inventores del cálculo pero representan un eslabón en una larga cadena iniciada muchos siglos antes.
• Fueron ellos quienes dieron a los procedimientos infinitesimales de sus antecesores inmediatos, Barrow y Fermat, la unidad algorítmica y la precisión necesaria como método novedoso y de generalidad suficiente para su desarrollo posterior.
• Estos desarrollos estuvieron elaborados a partir de visiones de hombres como Torricelli, Cavalieri, y Galileo; o Kepler, Valerio, y Stevin.
• Los alcances de las operaciones iniciales con infinitesimales que estos hombres lograron, fueron también resultado directo de las contribuciones de Oresme, Arquímedes y Eudoxo.
• Finalmente el trabajo de estos últimos estuvo inspirado por problemas matemáticos y filosóficos sugeridos por Aristóteles, Platón, Tales de Mileto, Zenón y Pitágoras. Para tener la perspectiva científica e histórica apropiada, debe reconocerse que una de las contribuciones previas decisivas fue la Geometría Analítica desarrollada independientemente por Descartes y Fermat.

Sin la contribución de éstos y de muchos otros hombres más, el cálculo de Newton y Leibniz seguramente no existiría. Su construcción fue parte importante de la revolución científica que vivió la Europa del siglo XVII. Los nuevos métodos enfatizaron la experiencia empírica y la descripción matemática de nuestra relación con la realidad. La revolución científica supuso una ruptura con las formas de pensar, estudiar y vincularse con la naturaleza que dominaron casi absolutamente en Europa entre los siglos V y XV. Esta ruptura y salto en la historia del conocimiento estuvieron precedidos por las importantes transformaciones que se vivieron durante los siglos XV y XVI con el Renacimiento y la Reforma Protestante. El Cálculo Diferencial e Integral están en el corazón del tipo de conocimiento, cultura y de sociedad de la que, esencialmente, somos parte.
Ecuaciones Diferenciales Ecuaciones Diferenciales O Ecuaciones diferenciales lineales
Ecuaciones diferenciales lineales, reducción del orden: Dada una solución y 1 (x) de la ecuación diferencial de segundo orden
y" + p(x)y' + q(x)y= 0(4.11)
puede determinarse una segunda solución y´´(x) que sea linealmente independiente con y 2 (x), de la forma v(x)y 1 (x), para cierta función v(x) distinta de una constante.
y'= y1v' + y'1v
y"= y1v" + 2y'1v' + y"1v.
Entonces Sustituyendo las expresiones anteriores para y, y' y y" en (4.11) y simplificando resulta.
(y1v" + 2y'1v' + y"1) + p(x) (y1v' + y'1v) + q(x)v = 0
v(y"1 + p(x)y'1 + q(x)y1) + v'(2y'1 + p(x)y1) + y1v" = 0
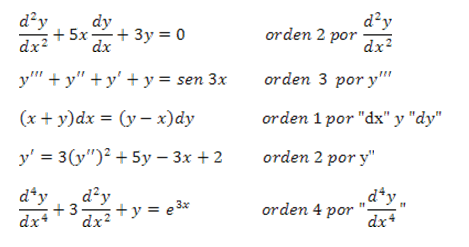

Probabillidad
Origen de la Probabilidad: La probabilidad nació gracias a los juegos de azar. En el Renacimiento empiezan a surgir inquietudes entorno a contabilizar el número de posibles resultados de un dado lanzado varias veces, o problemas más prácticos sobre cómo repartir las ganancias de los jugadores cuando el juego se interrumpe antes de finalizar. A los matemáticos del siglo XVI como Pacioli, Cardano y Tartaglia se deben las primeras consideraciones sobre los juegos de azar.
Rama de las Matemáticas que estudia los resultados posibles de los fenómenos aleatorios. Por ejemplo: El lanzamiento de una moneda, el lanzamiento de un dado, extracción de una carta de un mazo de naipes. Mide la frecuencia con la que se obtiene un resultado (o conjunto de resultados) al llevar a cabo un experimento aleatorio, del que se conocen todos los resultados posibles, bajo condiciones suficientemente estables.
Enfoque Clásico de Probabilidad La probabilidad de un evento es la razón entre el número de casos (sucesos) favorables y el numero total de casos (sucesos) posibles, siempre que nada obligue a creer que algunos de estos sucesos debe tener preferencia a los demás, lo que hace que sean igualmente posibles. La probabilidad de un evento A: P (A), es un NÚMERO, que mide el grado de certeza en el que un evento A ocurre, y se obtiene con la formula conocida como REGLA DE LA PLACE:
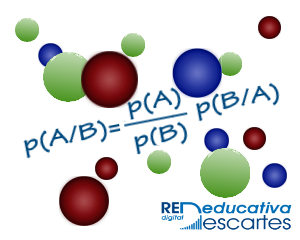

Enfoque de Frecuencia Relativa Si un experimento bien definido se repite n veces ( n grande); sea nA < n el número de veces que el evento A ocurre en los n ensayos, entonces la frecuencia relativa de veces que ocurre el evento A “n A /n”, es la estimación de la probabilidad que ocurra el evento A , o sea: P(A)= n A /n OBSERVACIONES: 1. La frecuencia relativa de un evento, esta comprendido entre 0 y 1. Por lo tanto 0 ≤ P(A) ≤ 1. En efecto: Desde que 0 ≤ n A ≤ 1 , 0/n ≤ n A /n ≤ 1 , se tiene que 0 ≤ n A /n ≤ 1 . Luego, 0 ≤ P(A) ≤ 1 . 2. n A /n = 0 , si solo si, en las n repeticiones del experimento el evento A .
- Dice que la probabilidad de ocurrencia de un evento es el grado de creencia por parte de un individuo de que un evento ocurra, basado en toda la evidencia a su disposición. Bajo esta premisa se puede decir que este enfoque es adecuado cuando solo hay una oportunidad de ocurrencia del evento. Es decir, que el evento ocurrirá o no ocurrirá esa sola vez. El valor de probabilidad bajo este enfoque es un juicio personal. Enfoque Subjetivo de Probabilidad.



No hay comentarios:
Publicar un comentario