GEOMETRÍA NO EUCLIDIANA: Se denomina geometría no euclidiana o no euclídea, a cualquier sistema formal de geometría cuyos postulados y proposiciones difieren en algún asunto de los establecidos por Euclides en su tratado Elementos. No existe un solo sistema de geometría no euclídea, sino muchos, aunque si se restringe la discusión a espacios homogéneos, en los que la curvatura del espacio es la misma en cada punto, en los que los puntos del espacio son indistinguibles, pueden distinguirse tres formulaciones1 de geometrías:
- La geometría euclidiana satisface los cinco postulados de Euclides y tiene curvatura cero (es decir se supone en un espacio plano por lo que la suma de los tres ángulos interiores de un triángulo da siempre 180°.).
- La geometría hiperbólica satisface sólo los cuatro primeros postulados de Euclides y tiene curvatura negativa (en esta geometría, por ejemplo, la suma de los tres ángulos interiores de un triángulo es inferior a 180°).
- La geometría elíptica satisface sólo los cuatro primeros postulados de Euclides y tiene curvatura positiva (en esta geometría, por ejemplo, la suma de los tres ángulos interiores de un triángulo es mayor a 180°).
Todos estos son casos particulares de geometrías riemannianas, en los que la curvatura es constante, si se admite la posibilidad de que la curvatura intrínseca de la geometría varíe de un punto a otro se tiene un caso de geometría riemanniana general, como sucede en la teoría de la relatividad general donde la gravedad causa una curvatura no homogénea en el espacio-tiempo, siendo mayor la curvatura cerca de las concentraciones de masa, lo cual es percibido como un campo gravitatorio atractivo.

HISTORIA
El primer ejemplo de geometría no euclidiana fue la hiperbólica, teorizada inicialmente por Immanuel Kant, formalizada posterior e independientemente por varios autores a principios del siglo XIX tales como Carl Friedrich Gauss, Nikolái Lobachevski, János Bolyai y Ferdinand Schweickard.
Los desarrollos de geometrías no euclídeas se gestaron en sus comienzos con el objetivo de construir modelos explícitos en los que no se cumpliera el quinto postulado de Euclides.
La geometría Euclidiana había sido desarrollada por los griegos y expuesta por Euclides en la obra Los elementos. En su primera obra publicada, "Pensamientos sobre la verdadera estimación de las fuerzas vivas"
Esas posibles geometrías que Kant entrevé son las que hoy se llaman geometrías euclidianas de dimensión mayor que 3.
Por otra parte, ya desde la antigüedad se consideró que el quinto postulado del libro de Euclides no era tan evidente como los otros cuatro pues, al afirmar que ciertas rectas (las paralelas) no se cortarán al prolongarlas indefinidamente, habla de una construcción mental un tanto abstracta. Por eso durante muchos siglos se intentó sin éxito demostrarlo a partir de los otros cuatro. A principios del siglo XIX, se intentó demostrarlo por reducción al absurdo, suponiendo que es falso y tratando de obtener una contradicción. Sin embargo, lejos de llegar a un absurdo se encontró que existían geometrías coherentes diferentes de la euclídea. Se había descubierto así la primera geometría no euclídea (en concreto el primer ejemplo que se logró era una geometría llamada hiperbólica).
Geometría hiperbólica
A principios del siglo XIX, y de modo independiente, Gauss (1777-1855), Lobachevsky (1792-1856), János Bolyai y Ferdinand Schweickard lograron construir la geometría hiperbólica, a partir del intento de negar el quinto postulado de Euclides y tratar de obtener una contradicción. En lugar de obtener una contradicción lo que obtuvieron fue una curiosa geometría en la que los tres ángulos de un triángulo sumaban menos de 180º sexagesimales (en la geometría euclídea los ángulos de cualquier triángulo suman siempre exactamente 180º).
La naturalidad de esta geometría quedó confirmada a finales del siglo, cuando Beltrami demostró que la geometría hiperbólica coincide con la geometría intrínseca de cierta superficie y Klein dio la interpretación proyectiva de la geometría hiperbólica. Ambos resultados prueban que es tan consistente como la geometría euclídea (es decir, si la geometría hiperbólica lleva a alguna contradicción, entonces la geometría euclídea también).
Algunos afirman que Gauss fue el primero en considerar la posibilidad de que la geometría del Universo no fuera la euclídea. Sabiendo que en la geometría hiperbólica la suma de los ángulos de cualquier triángulo es menor que dos ángulos rectos, se dice que subió a la cima de tres montañas con un teodolito, aunque la precisión de sus instrumentos no fue suficiente para decidir la cuestión con tal experimento. Sin embargo, otros afirman que cuando escribió que trataba de corregir los efectos de posibles curvaturas se refería a corregir el efecto de la curvatura terrestre en los estudios cartográficos que estaba realizando.

Geometría elíptica
La geometría elíptica es el segundo tipo de geometría no-euclídea homogénea, es decir, donde cualquier punto del espacio resulta indistinguible de cualquier otro. Una variedad de Riemann de curvatura positiva constante es un ejemplo de geometría elíptica. Un modelo clásico de geometría elíptica n-dimensional es la n-esfera.
En la geometría elíptica las líneas geodésicas tienen un papel similar a las líneas rectas de la geometría euclídea, con algunas importantes diferencias. Si bien la mínima distancia posible entre dos puntos viene dada por una línea geodésica, que además son líneas de curvatura mínima, el quinto postulado de Euclídes no es válido para la geometría elíptica, ya que dada una "recta" de esta geometría (es decir, una línea geodésica) y un punto no contenido en la misma no se puede trazar ninguna geodésica que no corte a la primera.
Geometría euclídea
La geometría euclídea es claramente un caso límite intermedio entre la geometría elíptica y la geometría hiperbólica. De hecho la geometría euclídea es una geometría de curvatura nula. Puede demostrarse que cualquier espacio geométrico o variedad de Riemann cuya curvatura es nula es localmente isométrico al espacio euclídeo y por tanto es un espacio euclídeo o idéntico a una porción del mismo.
Aspectos matemáticos
Los espacios de curvatura constante el tensor de curvatura de Riemann viene dado en componentes por la siguiente expresión:
GEOMETRÍA PROYECTIVA
Se llama geometría proyectiva a la rama de la matemática que estudia las propiedades de incidencia de las figuras geométricas, pero abstrayéndose totalmente del concepto de medida. A menudo se usa esta palabra también para hablar de la teoría de la proyección llamada geometría descriptiva.
Gérard Desargues es el iniciador de la geometría proyectiva, pues fundamentó matemáticamente los métodos de la perspectiva que habían desarrollado los artistas del Renacimiento, y aunque su trabajo fue publicado en 1639, pasó desapercibido durante dos siglos (excepto dos teoremas), ensombrecido por la influyente obra de Descartes.
En el siglo XIX, la geometría proyectiva y la geometría hiperbólica, se establecieron dentro de las matemáticas, pero lo que acabó de enraizarlas, posiblemente, fue hallar un modelo analítico. Dentro del contexto de la geometría euclidiana-cartesiana se puede construir la geometría proyectiva y, si se acepta la primera, hay que admitir la segunda.
Este proceso finalizó definitivamente a principios del siglo XX, pues Einstein, apoyándose en los exhaustivos desarrollos geométricos de los matemáticos del siglo XIX, consiguió demostrar que, a gran escala, el universo se puede interpretar mejor con estas nuevas geometrías que con el rígido espacio euclidiano.

PUNTO DE VISTA SINTÉTICO
Desde el punto de vista sintético, la geometría proyectiva es una geometría que parte de los siguientes principios:
- Dos puntos definen una recta.
- Todo par de rectas se cortan en un punto (cuando dos rectas son paralelas se dice que se cortan en un punto del infinito conocido como punto impropio).
El quinto postulado de Euclides, de las rectas paralelas, está implícito en estos dos principios ya que, dada una recta y un punto exterior, existirá una única recta paralela definida por el punto dado y el del infinito por el primer axioma.
Como los axiomas de los que se parte son simétricos, si en cualquier teorema proyectivo se intercambian las palabras recta y punto se obtiene otro teorema igualmente válido. A estos teoremas se les llama duales.
El principio antes expuesto se conoce como Principio de Dualidad y fue enunciado por Poncelet en el siglo XIX. Muchos teoremas anteriores, como los de Pascal y Brianchon, son duales, aunque ningún matemático lo había notado hasta entonces.
Los teoremas de Pascal y Brianchon, aunque completamente válidos, se demostraron inicialmente en geometría euclidiana, basándose en los teoremas de Pappus y Menelao, que utilizan una métrica y por tanto no son válidos en geometrías de incidencia, como la proyectiva.
En principio se intentó buscar demostraciones alternativas de estos teoremas sin usar congruencia de segmentos. Hilbert demostró en 1899 que tal cosa es imposible y desde entonces suele incluirse el teorema del hexágono de Pappus como un axioma de la geometría proyectiva. Ello permite demostrar en proyectiva todo lo demostrable en euclídea sin tener que recurrir a una métrica.
Por no usar métricas en sus enunciados, se dice que la geometría proyectiva es una Geometría de incidencia.
Finalmente, hay que destacar que desde el punto de vista sintético, un espacio proyectivo consiste en un espacio afín al que hemos añadido un conjunto de puntos infinitos, de modo que cada par de rectas paralelas se cortan en uno de estos puntos.
APLICACIONES
Cuando hacemos isomorfas nuestras paralelas euclídeas con las rectas proyectivas que se cortan “en el infinito”, podemos extrapolar todo lo que demostremos en proyectiva a geometría euclidiana. La geometría proyectiva, más flexible que la euclidiana, se convierte con esto en una herramienta útil para enunciar muchos teoremas clásicos más sencillamente, e incluso simplificar las demostraciones, aunque no permite demostrar nada que no pueda demostrarse en euclidiana.
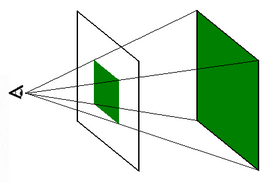
La geometría proyectiva puede entenderse, informalmente, como la geometría que se obtiene cuando nos colocamos en un punto, mirando desde ese punto. Esto es, cualquier línea que incide en nuestro "ojo" nos parece ser solo un punto, en el plano proyectivo, ya que el ojo no puede "ver" los puntos que hay detrás.
De esta forma, la geometría proyectiva también equivale a la proyección sobre un plano de un subconjunto del espacio en la geometría euclidiana tridimensional. Las rectas que llegan al ojo del observador se proyectan en puntos. Los planos definidos por cada par de ellas se proyectan en rectas.
Esto es útil porque a veces los teoremas de geometría proyectiva no pueden demostrarse solo con los axiomas de incidencia antes expuestos (Hilbert, 1899) y es necesario demostrarlos en geometría euclidiana y luego proyectar, como el teorema de Desargues (o bien admitir el teorema de Pappus anteriormente citado como axioma).
PUNTO DE VISTA VECTORIAL
La geometría proyectiva es el estudio del grupo de las proyectividades entre espacios proyectivos.
Axiomas
Sea un cuerpo y un -espacio vectorial (no trivial).
Llamaremos espacio proyectivo sobre V al conjunto cociente de por la relación de equivalencia anterior:
- .
Las rectas vectoriales de son conjuntos formados por los múltiplos escalares de los vectores no nulos, esto es, si , , la recta vectorial determinada por es el conjunto . La recta vectorial determinada por no es entonces otra cosa que el subespacio vectorial generado por , es decir, . El espacio proyectivo asociado a será el conjunto de todas las rectas vectoriales de .
Es inmediato que si , , entonces para cualquier tal que con , se cumple que las rectas vectoriales determinadas por y por coinciden, esto es, = . Ahí reside la esencia de un espacio proyectivo: consideramos solo las direcciones, no los vectores concretos. Ante este hecho, para trabajar solo con vectores y no con rectas vectoriales, se establece la siguiente relación, que resulta ser una relación de equivalencia: si , diremos que está relacionado con (lo escribiremos como ) si existe un de manera que . Al tomar el conjunto cociente se obtiene otra forma de definir .
Los elementos del espacio proyectivo serían entonces las clases de equivalencia de los vectores de mediante la relación de equivalencia .
Aun puede darse otro paso más para comprender mejor este tipo de espacios: Si tomamos una base de , como al tomar la recta vectorial generada por exigimos que , alguna de las coordenadas de respecto de la base tomada ha de ser necesariamente no nula. Al multiplicar escalarmente el vector no nulo por el inverso de esa coordenada no nula obtendremos otro vector de la misma recta vectorial, en el que ahora la coordenada no nula elegida va a valer 1. Como el nuevo vector está en la misma recta vectorial, su clase de equivalencia es la misma que la del vector antiguo, es decir, representa al mismo elemento del espacio proyectivo.
Veamos en un ejemplo qué significa esto:
Tomemos el espacio vectorial real (con la base canónica) y el vector no nulo .
Denotaremos por a su clase de equivalencia mediante la relación . Cuatro de las cinco coordenadas son no nulas, así que tenemos cuatro posibles maneras de realizar el proceso anterior: en el primer caso (dividiendo entre la primera coordenada, el 8) obtendríamos . Si en lugar de tomar la primera coordenada tomamos, por ejemplo, la quinta (), obtendríamos . Podríamos dividir las coordenadas del vector inicial entre las otras dos coordenadas no nulas, o , pero en todos los casos obtendríamos la misma clase de equivalencia, aunque las coordenadas no sean numéricamente las mismas. En esta situación se dirá que es la representación de la clase del vector en coordenadas homogéneas. Ha de quedar claro que
, y son coordenadas homogéneas del mismo punto proyectivo.
FUNDAMENTOS DE LA GEOMETRÍA
A finales del siglo XIX, la hegemonía de la geometría euclidiana había sido desafiada por la geometría no euclidiana y la geometría proyectiva. El primer intento notable de reorganizar el estudio de la geometría fue hecho por el matemático alemán Felix Klein y publicado en Erlangen en 1872. En su Programa de Erlanger, Klein propuso que la geometría euclidiana y no euclidiana se consideraran casos especiales de la geometría proyectiva. En cada caso, las características comunes que, según Klein, las hacían geometrías eran que había un conjunto de puntos, llamado “espacio”, y un conjunto de transformaciones mediante las cuales las figuras podían moverse en el espacio sin alterar su propiedades esenciales. Por ejemplo, en la geometría plana euclidiana el espacio es el plano familiar y las transformaciones son rotaciones, reflexiones, traslaciones y sus composiciones, ninguna de los cuales cambia ni la longitud ni el ángulo, las propiedades básicas de las figuras en la geometría euclidiana. Las diferentes geometrías tendrían diferentes espacios y diferentes grupos, y las figuras tendrían diferentes propiedades básicas.





























![[ (8, \frac{\pi}{3},0,2^{-15},\sqrt{7}) ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/04262be6be11f68257e0dd89f45026bba3dcef03)
![[(1,\frac{\pi}{24}, 0, 2^{-18},\frac{\sqrt{7}}{8})]](https://wikimedia.org/api/rest_v1/media/math/render/svg/d67cab9825d7c34e3671373f20e7b5e0b92fee66)

![[ (\frac{8}{\sqrt{7}}, \frac{\pi}{3 \sqrt{7}},0,\frac{2^{-15}}{\sqrt{7}} ,1) ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/551062d88cc3c9486f1f5c7d2cba25507bce453c)




